[Very Important Coding Interviews : Heap & Priority Queue#05] How To Solve ANY Heap & Priority Queue Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

Everything you MUST know to solve any Heap & Priority Queue question...

This is the best hands-on guide you will ever find on Heap & Priority Queue Technique which follows Pattern based Approach to Solve any Heap & Priority Queue question and Shortcuts You MUST READ and Implement.

Objective : Master all Heap & Priority Queue patterns that appear in 100% of coding interview problems.

---

Table of Contents

1. Introduction: Understanding Heaps and Priority Queues

2. Pattern 1: Top K Elements - Selection Problems

3. Pattern 2: Two Heaps - Median Finding

4. Pattern 3: Merge K Sorted - K-way Merge

5. Pattern 4: Scheduling with Heaps

6. Pattern 5: Stream Processing - Continuous Data

7. Pattern 6: Frequency-Based Heap

8. Pattern 7: Interval Management with Heaps

9. Advanced Patterns and Techniques

10. Company-Specific Problem Index

11. Interview Strategies and Templates

12. Shortcuts

Note : Each pattern comes with its Python Implementation ( can be found as you scroll) and at the end of thus post along with Heap & Priority Queue Shortcuts and problem examples.

—-

Practice your Interview with God Level Feedback Quantum —

https://quantumcoding.live/

On Quantum you can Practice FAANG-level questions with complete system design breakdowns, full architectures, trade-offs, and key concepts with God level feedback.

Also on live on product hunt - Quantum

Learn more patterns and shortcuts for each coding problem type —

How To Solve ANY Dynamic Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

- How To Solve ANY Backtracking Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

How To Solve ANY Greedy Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

How To Solve ANY Sliding Window Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

[Important : Upcoming Mass Layoffs Jan 2026] When and How to Prepare NOW ( Fast and Efficiently) ( With Implemented Projects)

Read ( major compilations of LLM System Design, ML System Design and 300+ Implemented Projects) —

[Important Bookmark Compilation] Complete Hands On LLM System Design Roadmap with Projects You MUST Follow (200000 Reads and Counting)

[Important] Compilation of Most Asked System Design, ML System Design Case Studies and LLM System Design

[Important Bookmark] Compilation of All Implemented Projects ( with Code Implementation Files)

---

Introduction: Understanding Heaps and Priority Queues

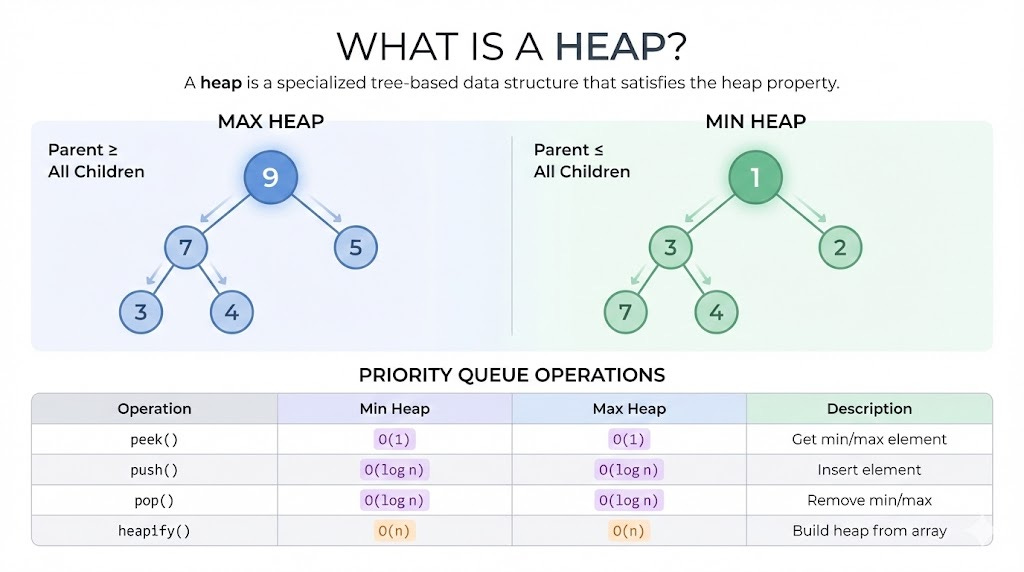
What is a Heap?

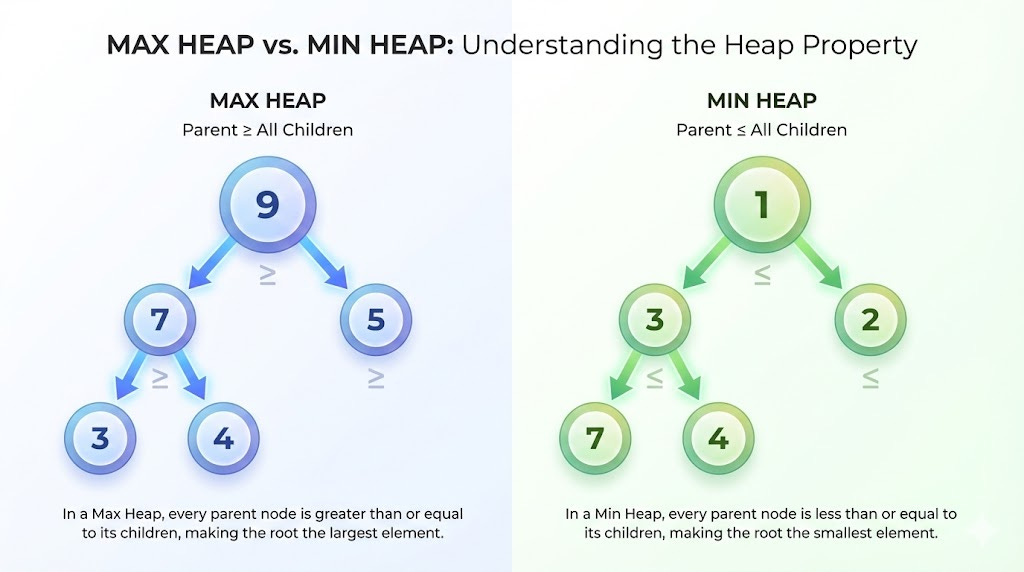
A heap is a specialized tree-based data structure that satisfies the heap property:

Max Heap:

Parent ≥ All Children
       9
      / \
     7   5
    / \
   3   4

Min Heap:

Parent ≤ All Children
       1
      / \
     3   2
    / \
   7   4

Priority Queue Operations

Operation Min Heap Max Heap

Description

peek() O(1) O(1) Get min/max element

push() O(log n) O(log n) Insert element

pop() O(log n) O(log n) Remove min/max

heapify() O(n) O(n) Build heap from array

---

Python’s heapq Module

Important: Python’s heapq is a MIN HEAP only!

import heapq

# Min Heap (default)
min_heap = []
heapq.heappush(min_heap, 5)
heapq.heappush(min_heap, 3)
heapq.heappush(min_heap, 7)
print(heapq.heappop(min_heap))  # 3 (smallest)

# Max Heap (negate values)
max_heap = []
heapq.heappush(max_heap, -5)
heapq.heappush(max_heap, -3)
heapq.heappush(max_heap, -7)
print(-heapq.heappop(max_heap))  # 7 (largest)

# Heapify existing list
nums = [3, 1, 4, 1, 5]
heapq.heapify(nums)  # O(n) - better than n insertions

---

When to Use Heaps— Deep Dive into Patterns, Implementations and Shortcuts: