[Very Important Coding Interviews: Trees and Advanced Trees#08] How To Solve ANY Trees and Advanced Trees Programming Question ( Pattern Approach with Shortcuts) : How it Works ( Implementation Code)

Everything you MUST know to solve any Trees and Advanced Trees question...

This is the best hands-on guide you will ever find on Trees and Advanced Trees which follows Pattern based Approach to Solve any Trees and Advanced Trees questions and Shortcuts You MUST READ and Implement.

Objective : Master all Trees and Advanced Trees patterns that appear in 100% of coding interview problems.

---

Table of Contents

1. Tree Traversal Patterns

2. Level Order Traversal (BFS)

3. Tree Height and Depth

4. Tree Diameter

5. Balanced Tree Validation

6. Same Tree and Subtree

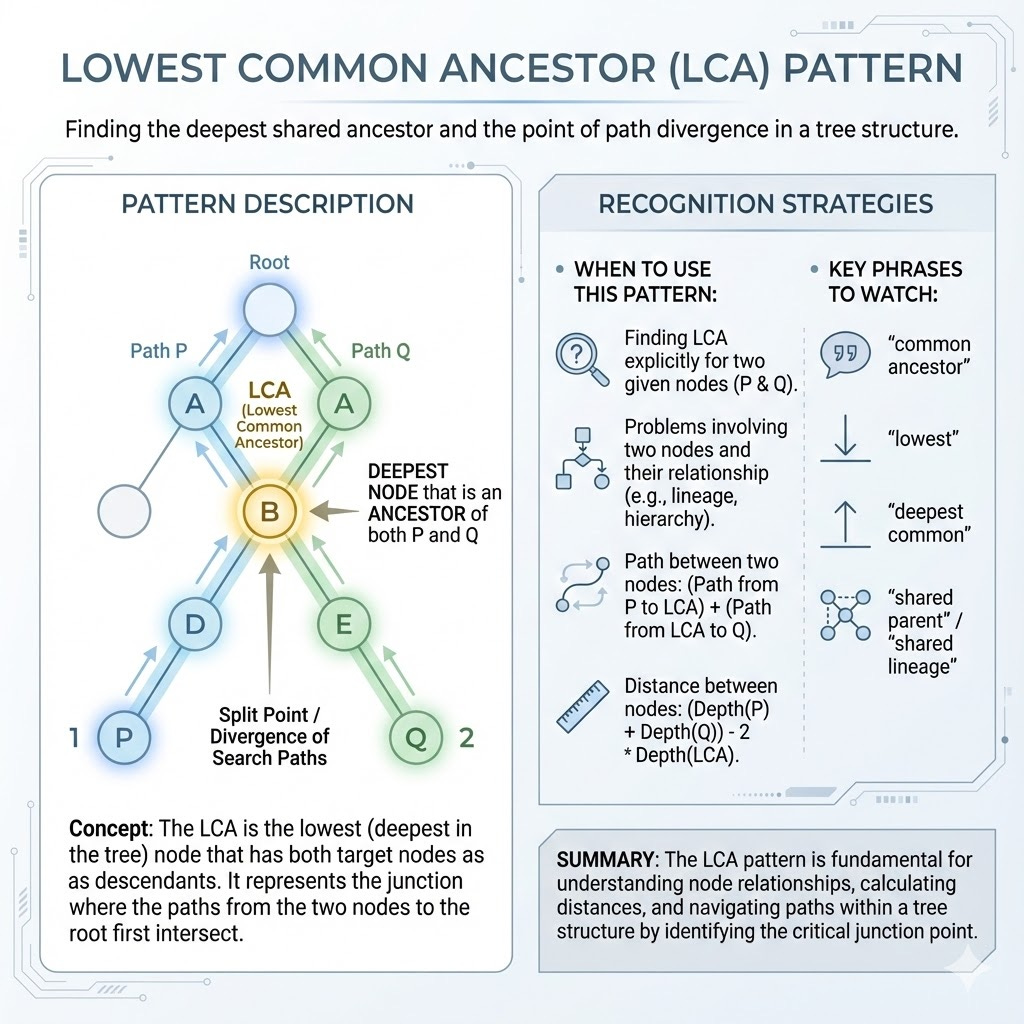
7. Lowest Common Ancestor (LCA)

8. Path Sum Patterns

9. Tree Construction

10. Serialize and Deserialize

11. Binary Search Tree (BST) Patterns

12. Trie (Prefix Tree)

13. Segment Tree

14. Binary Indexed Tree (Fenwick Tree)

15. Advanced Tree DP

Note : Each pattern comes with its Python Implementation ( can be found as you scroll) and at the end of thus post along with Trees and Advanced Trees Shortcuts and problem examples.

Practice your Interview with God Level Feedback Quantum —

https://quantumcoding.live/

On Quantum you can Practice FAANG-level questions with complete system design breakdowns, full architectures, trade-offs, and key concepts with God level feedback.

Also on live on product hunt - Quantum

Learn more patterns and shortcuts for each coding problem type —

How To Solve ANY Dynamic Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

- How To Solve ANY Backtracking Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

How To Solve ANY Greedy Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

How To Solve ANY Sliding Window Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

How To Solve ANY Heap & Priority Queue Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

How To Solve Stack and Advanced Stack Programming Question ( Pattern Approach with Shortcuts) : How it Works ( With Implementation Code)

How To Solve ANY Graph and Advanced Graph Programming Question ( Pattern Approach with Shortcuts) : How it Works ( Implementation Code)

[Important : Upcoming Mass Layoffs Jan 2026] When and How to Prepare NOW ( Fast and Efficiently) ( With Implemented Projects)

Read ( major compilations of LLM System Design, ML System Design and 300+ Implemented Projects) —

[Important Bookmark Compilation] Complete Hands On LLM System Design Roadmap with Projects You MUST Follow (200000 Reads and Counting)

[Important] Compilation of Most Asked System Design, ML System Design Case Studies and LLM System Design

[Important Bookmark] Compilation of All Implemented Projects ( with Code Implementation Files)

---

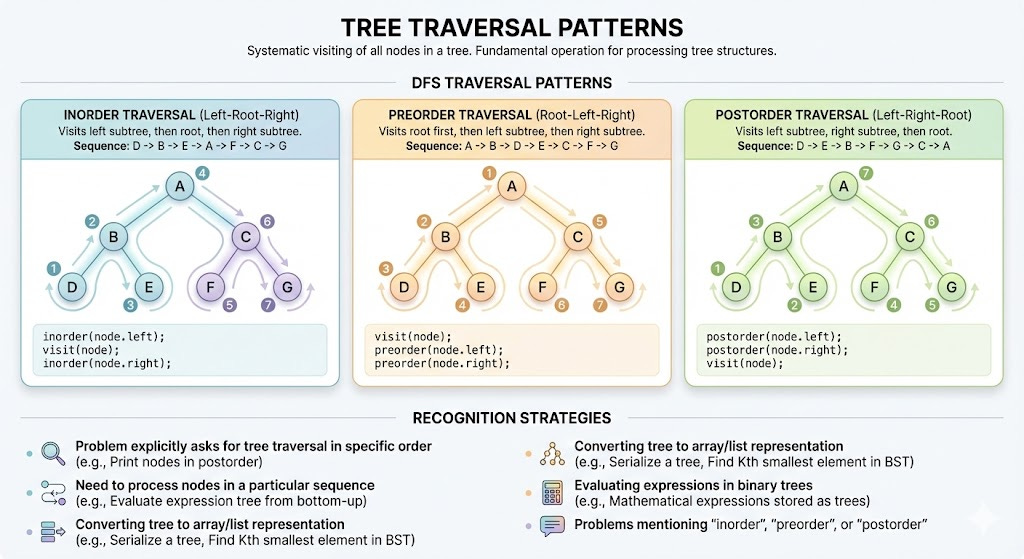
Tree Traversal Patterns

Pattern Description

Tree traversal is the fundamental operation of visiting all nodes in a tree systematically. The three main DFS traversal patterns are:

• Inorder (Left-Root-Right): Visits left subtree, then root, then right subtree

• Preorder (Root-Left-Right): Visits root first, then left subtree, then right subtree

• Postorder (Left-Right-Root): Visits left subtree, right subtree, then root

Pattern Recognition Strategies with Implementation and (many) shortcutts-